SeedSigner（シードの生成）

前回の記事で、hwwを「ビットコインを送金するための署名機」と表現しましたが、通常、hwwは署名をする前の行程もカバーします。

その流れを私たちが普段使っている銀行口座での例えを交えて説明します。

1. 乱数からシードを生成する。
2. シードから、秘密鍵と公開鍵を生成する。（秘密鍵はパスワード、公開鍵は口座番号のイメージです。）
3. 送金の際は秘密鍵を用いて取引の署名をする。（秘密鍵というパスワードを用いて口座振込をするイメージです。）

なお、上記の行程は内容を相当省いたものですので、例えを含めて正確性に欠けます。イメージとして流していただければと思いますが、ここで知っておいて欲しいことは、口座番号やパスワードといった取引の要となる情報は全てシードから生成されるということです。

本記事では、最初の「乱数からシードを生成」するまでの流れを解説していきます。その後、実際にSeedSignerを使って作業をしていきます。

エントロピーの生成

ビットコインを利用するために、まずは乱数を生成します。この乱数はいわば生物学におけるDNAのようなもので、ビットコインシステムにおける一意性を決める起点となるものです。この乱数は「天文学的に大きな数値」であり、その使用目的から、他者に予測されづらいランダム性を有する必要があります。

この予測困難なランダム性のことを「エントロピー」と言いますが、ビットコインの文脈においては、ここで作成する128〜256bitの乱数のことを「エントロピー」と言います。なお、今回は256bitのエントロピーをSeedSignerで生成する前提で説明をします（128bitでも十分なセキュリティはあるようですが、256bitが推奨されているためです）。

乱数の生成

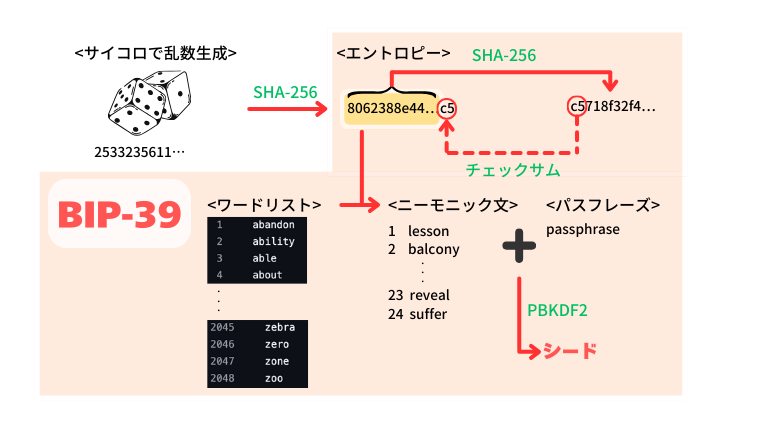
まずはエントロピーの元になる乱数を作ります。これにはたくさんのやり方がありますが、おすすめはサイコロを使う方法です。

SeedSignerでは256bitのエントロピーを生成するにあたって、高いランダム性を確保ために99回サイコロを振るようになっています。

乱数の文字列を256bit長のエントロピーに変換

ここからの処理は、「BIP-39」という基準に沿って説明していきます。BIPとは「Bitcoin Improvement Proposal」の略で、文字通りビットコインの運用における改善提案が標準化されたものです。このうち、BIP-39とはニーモニック文（後述します。）を使ったウォレットのバックアップ方法を規定した内容となります。

まず先ほど作った99個のサイコロの出目を256bit（256個の0と1の羅列）に変換します。

この変換のために、出目の文字列を「暗号学的ハッシュ関数（cryptographic hash）」の一種である「SHA-256」を使って変換（「ハッシュ化」）します。

SHA-256はビットコインにおいて重要な役割を果たす関数です。このアルゴリズム自体を覚える必要はありませんが、暗号学的ハッシュの特徴は押さえておく必要があります。

暗号学的ハッシュ

入力データ（「原像（pre-image）」と呼びます）から暗号学的ハッシュ（以下の特徴を有する固定長の出力値、以後「ハッシュ値」といいます）を生成する関数のことを「暗号学的ハッシュ関数（cryptographic hash function）」といいます。

簡単に言うと「ある入力データを、暗号学的な特徴を有する特定の長さのビット列に変換する関数」を言います。

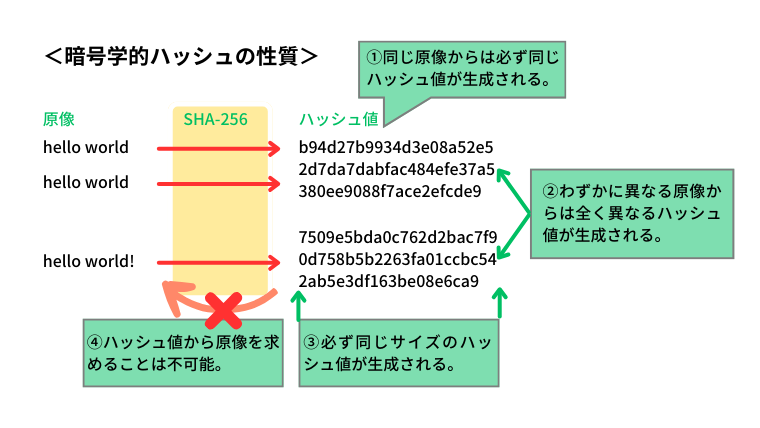
ハッシュ値には以下の性質があります。

1. 同じ原像からは必ず同じハッシュ値が生成される。
2. わずかに異なる原像からは全く異なるハッシュ値が生成される。
3. 必ず同じサイズのハッシュ値が生成される。
4. ハッシュから原像を求めることは現実的に不可能。（出力にこのような性質を付与する関数を「一方向性関数（one-way funcition）」といいます。）

特に④の特徴を満たすには以下の特性を有する必要があります。

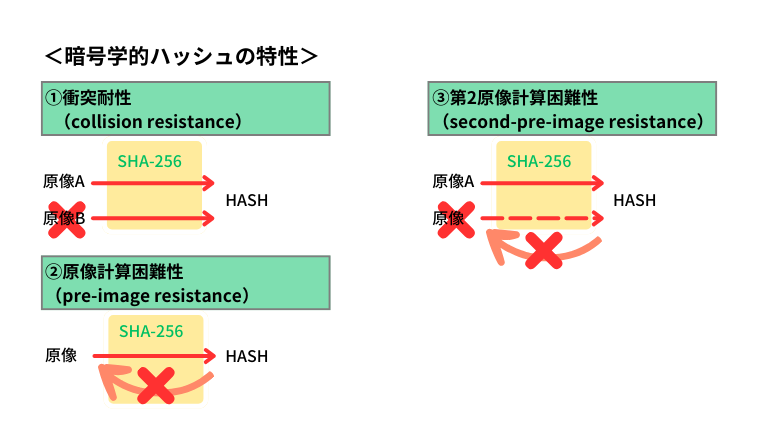
1. 衝突耐性（collision resistance）：ハッシュ関数のみが判明している場合、同じハッシュ値が出力される異なる入力を見つけることは（天文学的に）困難です。
2. 原像計算困難性（pre-image resistance）：ハッシュ関数とハッシュ値が判明している場合、ハッシュの現像を見つけることは（天文学的に）困難です。
3. 第2原像計算困難性（second-pre-image resistance）：ハッシュ関数と1つの原像が判明している場合、同じハッシュ値を出力する別の現像を見つけることは（天文学的に）困難です。

細かい特徴を書いてきましたが、極端に言うと「入力データがちょっとでも書き換えられるとハッシュ値は全く異なる値になる」、「ハッシュ値から入力データを再現することは不可能」、「同じハッシュ値となる異なる入力データは存在しない」ということです。

SHA-256

そしてビットコインではSHA-256（「Secure Hash Algorithm with 256-bit output」の略）という暗号学的ハッシュ関数が多用されています。

SHA-256のアルゴリズムの詳細は省略しますが、パディング（桁数を合わせるために数値を詰める）、分割・結合、シフト演算、論理演算等を組み合わせ、特定の手順でごちゃ混ぜにした上で、最終的に256bitの出力を得る操作を行なっています。

では実際に、サイコロの出目をSHA-256でハッシュ化してみます。ターミナルに以下のコマンドを入力することでハッシュ値を計算することができます。

# echoコマンド：文字列を表示するコマンド。「-n」オプションで改行を無視する。
# パイプ「|」は、左側のコマンドの標準出力を右側のコマンドの標準入力とする。
# shasumコマンド：SHA-2のハッシュ値を計算する。「-a」（--algorithmの略）オプションで種類を指定、「-a 256」でSHA-256となる。
% echo -n 253323561122445142522153333554661623423431156553331133246543333221665235442611345332421115452233243 | shasum -a 256
8062388e442ae9800ca94175a8007c526442f434d80d9b0da26ce852ff7eae1e  -

 

これで256bitのエントロピーを得ることができました。

エントロピーは数字の羅列で非常に扱いにくいという問題があります。そのため、BIP-39では、人が覚えやすい一連の単語にエントロピーを変換していく手順が規定されています。この一連の単語のことを「ニーモニック文（mnemonic sentence）」と言います。

チェックサムの付加

エントロピーをニーモニック文に符号化する際、エントロピーを11bit毎に10進数に変換し、その数字をインデックスとして2048種類（11bitは２^11=2048まで表せる）ある単語に置き換えます。

ただし、「256bit/11bit=23余り3」となるため、最後の1単語で8bit分足りていません。そこで8ビット分を「チェックサム（検証用符号）」としてエントロピーの末尾に追加します。

チェックサムは、エントロピーをバイナリデータ（0と1の2進数データ）としてハッシュ化し、最初の8bitを採用します。

# -nオプション以下の「1000...1110」はエントロピーを2進数変換したデータです。
# 最後の「-0」（--01の略）オプションは、ビットモードでの入力を指定する（ビット列として処理する）。
% echo -n 1000000001100010001110001000111001000100001010101110100110000000000011001010100101000001011101011010100000000000011111000101001001100100010000101111010000110100110110000000110110011011000011011010001001101100111010000101001011111111011111101010111000011110 |  shasum -a 256 -0
c5718f32f4033c7907db00318f321e089c11db3540e0ab2b9da93d14efd8f858 ^-

 

今回の場合、最初の16進数2桁である「c5」がチェックサムとなります。

ニーモニック文への符号化

それでは、エントロピー+チェックサムを11bit毎に分け、10進数に変換し、2048種類の単語に置き換えます。

①エントロピーにチェックサムを追加
8062388e442ae9800ca94175a8007c526442f434d80d9b0da26ce852ff7eae1ec5
↓
②2進数に変換
1000 0000 0110 0010 0011 1000 1000 1110 0100 ...（省略）... 1110 1100 0101
↓
③11bit毎に分ける
10000000011 00010001110 00100011100 ...（省略）... 11011000101
↓
④10進数に変換
1027 142 284 ...（省略）... 1530 1475 1733

 

11bitは0から2047、BIP-39のワードリストは1から2048で付番されています。1だけずらして変換するので注意してください。

1単語目は1028番目の単語、2単語目は143番目の単語・・・と置き換えていくと、次の24単語に変換できます。これをニーモニック文と言います。

⑤次の24単語に変換できる
lesson balcony castle marriage purse scale crawl choice interest divorce business pill during key square accuse only home open spawn copper satisfy reveal suffer

 

パスフレーズの追加

ニーモニック文に加えて、追加の「パスフレーズ」を設定することもできます。これは任意の文字列であり、セキュリティを強化するためのパスワード（または任意の25単語目）のような役割を果たします。

次はニーモニック文とパスフレーズをシードに変換するのですが、自分のビットコインを管理するには、ニーモニック文及びパスフレーズをバックアップとして記録します。そして、シードへの変換はhww内で行われるので、普段シードを目にすることはありません。

なお、エントロピーの生成〜ニーモニック文への符号化（及びパスフレーズの付与）まで、hwwで簡単に行うことができます。にもかかわらず、あえて細かい手順について説明をしてきたのは、欲を言えば、ニーモニック文の生成も検証して欲しいからです。

説明してきたようにパソコンで計算しても良いですし、SeedSignerであれば２台用意して同じサイコロの出目から同じニーモニック文が生成されるか確認したいところです。

ニーモニック文はビットコイン管理のバックアップとなりますので、hwwにバックドアが仕込まれており、生成されたニーモニック文が仕組まれたものであったとしたら最悪です。そのため、ニーモニック文の生成についても検証してみることをお勧めします。

シードの生成

最も大事な部分はニーモニック文の生成までのアルゴリズムになりますが、ここではニーモニック文及びパスフレーズからシードを生成する方法についても、概要をまとめておきます。

シードの生成には「PBKDF2（Password-Based Key Derivation Function 2）」という関数を使用します。

PBKDF2

PBKDF2では以下のデータを設定します（BIP-39における設定値です）。

• パスワード：ニーモニック文（例："lesson balcony ..."）
• ソルト：「mnemonic」+パスフレーズ（例：パスフレーズが「password」の場合、"mnemonicpassword"）
• 反復回数：2048回
• ハッシュ関数：HMAC-SHA512
• 出力長：512bit

次に、パスワードとソルトを合わせてHMAC-SHA512で反復回数分ハッシュ化を繰り返します。具体的には次のような手順となります。

1. 1回目：「パスワード、ソルト、1（正確には16進数で「00000001」）」を連結したデータを、HMAC-SHA512でハッシュ化（ハッシュ値をH1とします。）。
2. 2回目：「パスワード、H1」を連結したデータを、HMAC-SHA512でハッシュ化（ハッシュ値をH2とします。）。
3. 3回目以降：「パスワード、H2」を連結したデータを、HMAC-SHA512でハッシュ化（ハッシュ値をH3とします。）。以降、「パスワード、一つ前のハッシュ値」を連結したデータのハッシュ化を、2048回繰り返します。
4. 最後に、H1 XOR H2 XOR , ... , XOR H2048を計算します。※（XOR（排他的論理和）：2つの入力のうち片方のみが1であるときのみ出力が1となり、両方1や両方0の場合は0となる）

これにより、512bitのシードを生成することができます。